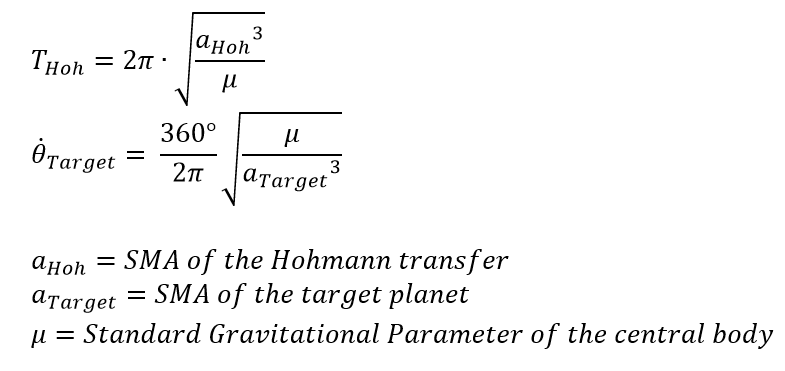
For the Hohmann transfer, we demand that: Rearranging, the required fractional change in velocity from the first impulse is So we can get the rocket to reach the height for an instant, but we need a second impulse to keep it there and circularise the orbit. Say this requires an additional change in velocity. A Hohmann Transfer is a two-impulse elliptical transfer between two co-planar circular orbits. The transfer itself consists of an elliptical orbit with a perigee at.
Hohmann transfers are not just for Earth orbiting spacecraft - they can also be used for interplanetary transfers. Calculating an interplanetary Hohmann transfer is very similar to calculating a Hohmann transfer for an Earth orbiting spacecraft. The only difference we have is that we have one more thing to calculate: The necessary phase angle for the two planets.
In this section, we will cover:
1.Calculating an Interplanetary Hohmann Transfer
2.Modeling an Interplanetary Hohmann Transfer
Calculating an Interplanetary Hohmann Transfer
Calculating the Δv required for an interplanetary Hohmann transfer is exactly like how we did it in the Hohmann Transfer tutorial. Our 'parking' orbit SMA is actually our departure planet's SMA about the Sun. Our 'target' orbit SMA is the arrival planet's SMA about the Sun.
However, like the Hohmann Transfer tutorial, we must assume that the two planets are both circular and co-planar. Since this definitely isn't the case with any of our solar system's planets in the real world, these calculations only present a conceptual idea of the amount of Δv required for an interplanetary transfer.
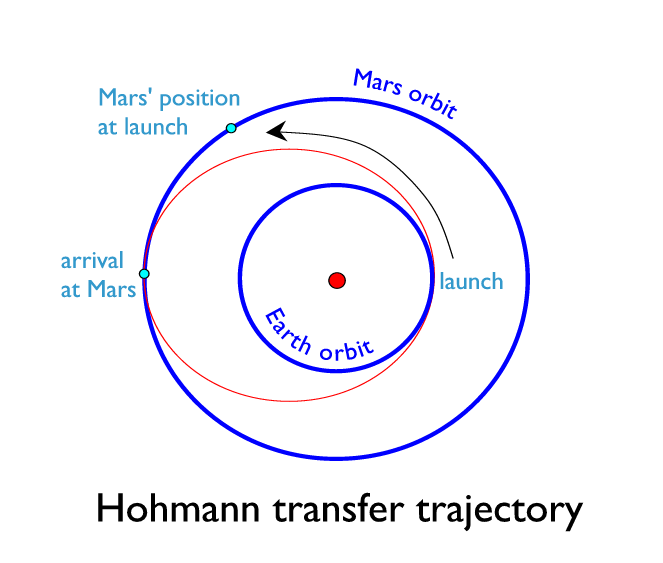
One more thing we need to do in addition to the Δv calculations is calculating the necessary phase angle between the planets. The planets need to be at a certain position relative to each other so that when the interplanetary spacecraft reaches the other side of the Hohmann transfer, the arrival planet is there as well. The phase angle 'Φ' is shown here:
Phase Angle Diagram
You can calculate the phase angle using the following formula:
For this formula, you need the period of the Hohmann transfer, and the angular velocity of the target planet. What we are essentially doing is finding how many degrees the target planet will travel during the time of the Hohmann transfer, which is half of the Hohmann transfer period. To calculate the period of the Hohmann transfer and the angular velocity of the target orbit, we need the following formulas:
It is important to note that the formula for the angular velocity is only true when dealing with a circular orbit. Because our interplanetary Hohmann transfer assumes a perfectly circular orbit for both planets, we can use this formula.
Modeling an Interplanetary Hohmann Transfer
When calculating Hohmann transfers, we must first assume that both orbits are circular. In the real world, the orbits of Earth and Mars are not circular. So to model an interplanetary Hohmann transfer, we will be using Spacecraft in heliocentric circular orbits with the same SMA as the planets they are representing. Because basic interplanetary Hohmann transfers only rely on the gravity of the central body, we do not need to model the departure and arrival planets' gravities in our problem.
Problem: Assume that Earth and Mars are in circular orbits around the Sun at 1 AU and 1.524 AU, respectively. How much Δv is required to perform a Hohmann transfer to Mars? How many days would this transfer take? |
•Create a new Mission Plan and save it as 'InterplanetaryHohmann.MissionPlan'
Adding in Spacecraft
•Create a Spacecraft with the following elements:
oCentral Body: 'Sun'
oReference Frame: 'Mean of J2000 Earth Ecliptic'
Hohmann Transfer Orbit Pdf
oA: 149,597,871 km (This is 1 AU)
oE: 0
oI: 0 deg
oRAAN: 0 deg
oW: 0 deg
oTA: 0 deg
NOTE: Remember that you need to change the Element Type to 'Keplerian' to access these elements
•Rename the Spacecraft to 'InterplanetarySC'
•Click on the 'Force Model' on the left-hand side

•Uncheck the 'Earth' and 'Moon' boxes
•Click on 'Propagator' on the left-hand side
•Change the step size to 1 day
•Click 'Ok' to close the editor
•Clone 'InterplanetarySC'
•Rename the clone to 'MarsSC' (this Spacecraft will represent Mars)
•Change A to 227,987,155 km (This is 1.524 AU)
•Click on 'Visualization' on the left-hand side
•Change the tail color to green
•Click 'Ok' to close the editor
Adding in the ViewWindow
•Create a ViewWindow through the Object Browser
•Double click on 'ViewWindow1' to open the editor
•Check each Spacecraft in the 'Available Objects'
•Click on 'Spacecraft' in the 'Available Objects' to select both Spacecraft, then check 'Show Name'
•Change the history mode to 'Unlimited' (for both Spacecraft)
Since we won't be needing to show the real Earth and the real Mars, let's hide them from the ViewWindow.
•Click on the 'Solar System' section on the left-hand side
•Click on 'Earth'
•Uncheck 'Show Object' in 'Object Options'
Hohmann Transfer Orbit Animation
•Click on 'Mars'
•Uncheck 'Show Object' in 'Object Options'
Solar System Properties in the ViewWindow Editor
Now we can continue with the rest of the settings for the ViewWindow.
•Click on 'Viewpoints' on the left-hand side
•Change the reference frame to 'Inertial'
•Change the Source to 'Sun'
•Click 'Copy to Target/Tail Ref.'
•In 'Source Offsets', change the radius to 500,000,000 km
•Click 'Ok' to close the editor
Adding an ImpulsiveBurn
•Create an ImpulsiveBurn object through the Object Browser
•Double-click on 'ImpulsiveBurn1' to open the editor
•Change the attitude system to 'VNB'
•Click 'Ok' to close the editor
Building the Mission Sequence
To start, we'll propagate the entire solar system for a while so we can see each planet's orbit better.
•Drag and drop a while loop into the Mission Sequence
•Change the while loop argument to '(InterplanetarySC.ElapsedTime < TIMESPAN(500 days))'
•Drag and drop a FreeForm script editor inside that while loop
•Open the script editor and rename it to 'Step and Update'
In this script, we will step both Spacecraft with an epoch sync, and update the ViewWindow. To do this, we write:
// Steps both spacecraft with an epoch sync Step InterplanetarySC; Step MarsSC to (MarsSC.Epoch InterplanetarySC.Epoch); // Updates the ViewWindow Update ViewWindow1; |
Let's go back to the Mission Sequence.
•Drag and drop a FreeForm script editor after the while loop
•Open the script editor and rename it to 'Calculate Hohmann Delta V'
In this FreeForm script editor, we will calculate the necessary Δv needed and assign it to the ImpulsiveBurn object we created. To do this, we write:
// SMAs of the departure and arrival planets Variable startingOrbit = InterplanetarySC.A; Variable arrivalOrbit = MarsSC.A; // SMA of the Hohmann transfer Variable transfSMA = (startingOrbit + arrivalOrbit)/2; // Velocity of the Hohmann transfer at Periapsis Variable vTransfPeri = sqrt(Sun.Mu * ((2/startingOrbit) - (1/transfSMA))); // Delta V for the Hohmann transfer Variable dV1 = vTransfPeri - InterplanetarySC.VMag; ImpulsiveBurn1.BurnDirection[0] = dV1; |
Next, we need to calculate the phase angle. Let's add another FreeForm script editor to the Mission Sequence.
•Drag and drop a FreeForm script editor after the 'Calculate Hohmann Delta V' FreeForm
•Open the script editor and rename it to 'Calculate Phase Angle'
In this script, we need to calculate the necessary phase angle for the Hohmann transfer. To do this, we can use the formulas given in the Calculating an Interplanetary Hohmann Transfer section. We will need to write:
Variable Pi = acos(-1); // Period of the Hohmann transfer Variable THoh = 2 * Pi * sqrt(transfSMA^3/Sun.Mu); // Angular Velocity of the Target Planet Variable angVelTarget = (360/(2 * Pi)) * sqrt(Sun.Mu/(arrivalOrbit^3)); // Phase Angle Variable phaseAngle = 180 - (1/2) * (THoh * angVelTarget); |
Now that we've calculated the phase angle, we should try and calculate another very helpful thing: the next epoch at which this phase angle occurs. To do this, we will need to calculate two things: the current phase angle, and the phase angular velocity (the rate at which the phase angle changes).
The current phase angle is pretty easy to calculate. If we take the position vectors of each Spacecraft and use the 'VertexAngle' method, we can calculate the angle between the two.
Hohmann Transfer Orbit Mars
// Current Phase Angle Variable currentPhaseAngle = InterplanetarySC.Position.VertexAngle(MarsSC.Position); |
However, this method will not return a value greater than 180 degrees. If Earth is ahead of Mars, we need to add 180 degrees to the phase Angle. To do this, we can take the z component of the cross product of InterplanetarySC.Position and MarsSC.Position, and check to see if it's negative. If it is, that means we need to add 180 degrees. To do this, we write:
// If Earth is in front of Mars, add 180 degrees to the current phase angle If(InterplanetarySC.Position.CrossProduct(MarsSC.Position)[2] < 0) then; currentPhaseAngle += 180; End; |
Now, we need to calculate the phase angular velocity. In this scenario, this will simply be the difference between Earth's angular velocity and Mars's angular velocity. To calculate this, we write:
// Starting Planet Angular Velocity Variable angVelStarting = (360/(2 * Pi)) * sqrt(Sun.Mu/(startingOrbit^3)); // Phase Angular Velocity Variable angVelPhase = angVelStarting - angVelTarget; |
Now that we have the phase angular velocity, we can calculate how long it will take until we've reached our departure position. To calculate this, we take the difference of our current phase angle, and our departure phase angle. If we divide this difference by the phase angular velocity, we will have the amount of time (in seconds) until we've reached our departure position. Then, we can add that to our current epoch to calculate the departure epoch. To do this, we write:
// Time until Departure Variable timeTilDep = (currentPhaseAngle - phaseAngle)/angVelPhase; // Departure Epoch TimeSpan departureEpoch = InterplanetarySC.Epoch + TimeSpan.FromSeconds(timeTilDep); |
We have done all the necessary calculations for our first maneuver. Now, we need to step to the departure date, maneuver, then step to the arrival date. Let's go back to the Mission Sequence.
•Drag and drop a FreeForm script editor after the 'Calculate Phase Angle' FreeForm
•Open the script editor and rename it to 'Step to Departure, Maneuver, Step to Arrival'
In this script, we will step to the departure epoch, maneuver the Spacecraft, change the Spacecraft tail color for a better visualization, calculate the arrival epoch, and step to the arrival epoch. To do this, we write:
// Steps to the departure time While(InterplanetarySC.Epoch < departureEpoch); Step InterplanetarySC; Step MarsSC; Update ViewWindow1; End; // Maneuvers the spacecraft for the Hohmann transfer Maneuver InterplanetarySC using ImpulsiveBurn1; // Changes the tail color of the spacecraft InterplanetarySC.Color = ColorTools.Cyan; // Arrival Epoch TimeSpan arrivalEpoch = InterplanetarySC.Epoch + TimeSpan.FromSeconds((1/2)*(THoh)); // Step to Arrival While(InterplanetarySC.Epoch < arrivalEpoch); Step InterplanetarySC; Step MarsSC; Update ViewWindow1; End; |
The last thing we need to do for this transfer is to match our speed with our target. Let's go back to the Mission Sequence.
•Drag and drop a FreeForm script editor after the 'Step to Departure, Maneuver, Step to Arrival' FreeForm
•Open the script editor and rename it to 'Orbit Matching Maneuver'
In this script, we will need to calculate speed of Mars's orbit, calculate the Δv required to match the orbit, maneuver the spacecraft, then propagate for 300 days to visualize this change. To do this, we write:
// Velocity of Mars orbit Variable vMarsOrbit = sqrt(Sun.Mu * ((2/arrivalOrbit) - (1/arrivalOrbit))); // Delta V required for maneuver Variable dV2 = vMarsOrbit - InterplanetarySC.VMag; ImpulsiveBurn1.BurnDirection[0] = dV2; Maneuver InterplanetarySC using ImpulsiveBurn1; // Propagates SC for 300 days While(InterplanetarySC.ElapsedTime < TIMESPAN(300 days)); Step InterplanetarySC; Step MarsSC to (MarsSC.Epoch InterplanetarySC.Epoch); Update ViewWindow1; End; |
One more thing we need to add to the script - the thing we've been looking for all along! We need to report the Δv, and the time of flight in days. For the time of flight, we can simply take the difference of the arrival epoch and the departure epoch as these are measured in days. To report these values, we write:
Report (dV1 + abs(dV2)), (arrivalEpoch - departureEpoch).ToDays(); |
Your Mission Sequence should look something like this:
Mission Sequence Example
Save and run your Mission Plan, then try and answer these questions:
How much total Δv was required for the transfer?
How many days did the transfer take?
Try reporting the distance between the two spacecraft at the time where InterplanetarySC 'meets' MarsSC (right before the orbit matching maneuver). To do this, you can add the command 'Report InterplanetarySC.RadialSeparation(MarsSC)' right before the command to perform the second maneuver. About how far apart were the Spacecraft?
See Also
•Interplanetary Topics
•Next Topic: Patched Conics Transfer

Comments are closed.